Абстрактні структури.

Множини

Тип даних „множина” не реалізований як стандартний тип мови програмування С/С++, але дуже часто використовується в програмуванні і реалізовується засобами визначення типів користувача, тому дамо йому короткий опис.

Множина - така структура, яка є набором даних одного і того ж типу, що не повторюються (кожен елемент множини є унікальним). Порядок слідування елементів множини на має принципового значення.

До множин застосовується стандартний принцип виключення. Це означає, що конкретний елемент або є членом множини, або ні. Множина може бути пустою, таку множину називають нульовою.

Множина є підмножиною іншої множини, якщо в цій другій множині можна знайти усі елементи, які є в першій множині. Відповідно, множина вважається надмножиною іншої множини, якщо вона містить усі елементи цієї другої множини.

Кожен окремий елемент є членом множини, якщо він входить до складу елементів множини.

Над множинами визначені наступні специфічні операції:

Об’єднання множин. Результатом є множина, що містить елементи початкових множин.
Перетин множин. Результатом є множина, що містить спільні елементи початкових множин.
Різниця множин. Результатом є множина, яка містить елементи першої множини, які не входять в другу множину.
Симетрична різниця. Результатом є множина, яка містить елементи, які входять до складу однієї або другої множини (але не обох).
Перевірка на входження елемента в множину. Результатом цієї операції є значення логічного типу, що вказує чи входить елемент в множину.

Діаграми Ейлера для операцій над множинами

Таблиці

Елементами векторів і масивів можуть бути інтегровані структури. Одна з таких складних структур - таблиця. З фізичної точки зору таблиця є вектором, елементами якого є структури. Характерною логічною особливістю таблиць є те, що доступ до елементів таблиці проводиться не за номером (індексом), а за ключем - значення однієї з властивостей об’єкту, який описується структурою-елементом таблиці. Ключ - це властивість, що ідентифікує дану структуру в множині однотипних структур і є, як правило, унікальним в даній таблиці. Ключ може включатися до складу структури і бути одним з його полів, але може і не включатися в структуру, а обчислюватися за деякими її властивостями. Таблиця може мати один або декілька ключів.

Основною операцією при роботі з таблицями є операція доступу до структури за ключем. Вона реалізовується процедурою пошуку. Оскільки пошук може бути значне більш ефективним в таблицях, впорядкованих за значеннями ключів, досить часто над таблицями необхідно виконувати операції сортування.

Іноді розрізняють таблиці з фіксованою і із змінною довжиною структури. Очевидно, що таблиці, які об’єднують структури ідентичних типів, будуть мати фіксовані довжини структур. Необхідність в змінній довжині може виникнути в задачах, подібних до тих, які розглядалися для об’єднань. Як правило таблиці для таких задач і складаються із структур до складу яких входять об’єднання, тобто зводяться до фіксованої (максимальній) довжини структури. Значно рідше зустрічаються таблиці з дійсно змінною довжиною структури. Хоча в таких таблицях і економиться пам’ять, але можливості роботи з такими таблицями обмежені, оскільки за номером структури неможливо визначити її адресу. Таблиці із структурами змінної довжини обробляються тільки послідовно - в порядку зростання номерів структур. Доступ до елемента такої таблиці звичайно здійснюється в два кроки. На першому кроці вибирається постійна частина структури, в якій міститься, - в явному чи неявному вигляді - довжина структури. На другому кроці вибирається змінна частина структури у відповідності з її довжиною. Додавши до адреси поточної структури її довжину, одержують адресу наступної структури.

Стеки

Стеком називається множина деякої змінної кількості даних, над якою виконуються наступні операції:

Поповнення стеку новими даними;
Перевірка, яка визначає чи стек пустий;
Перегляд останніх доданих даних;
Знищення останніх доданих даних.

На основі такого функціонального опису, можна сформувати логічний опис. Стек - це такий послідовний список із змінній довжиною, включення і виключення елементів з якого виконуються тільки з одного боку списку. Застосовуються і інші назви стеку - магазин, пам’ять що функціонує за принципом LIFO (Last-In-First-Out - „останнім прийшов - першим вийшов”).

Схематичне зображення стеку

Самий„верхній” елемент стеку, тобто останній добавлений і ще не знищений, відіграє особливу роль: саме його можна модифікувати й знищувати. Цей елемент називають вершиною стеку. Іншу частину стеку називають тілом стеку. Тіло стеку, само собою, є стеком: якщо виключити зі стеку його вершину, то тіло перетворюється в стек.

Основні операції над стеком - включення нового елемента (push - заштовхувати) і виключення елемента зі стеку (pop - вискакувати).

Корисними можуть бути також допоміжні операції:

визначення поточної кількості елементів в стеку;
очищення стеку;
„неруйнуюче” читання елемента з вершини стека, яке може бути реалізоване, як комбінація основних операцій -виключити елемент зі стеку та включити його знову в стек.

При представленні стеку в статичній пам’яті для стеку виділяється пам’ять, як для вектора. В описі цього вектора окрім звичайних для вектора параметрів повинен знаходитися також покажчик стеку - адреса вершини стека. Обмеження даного представлення полягає в тому, що розмір стеку обмежений розмірами вектора.

Покажчик стеку може вказувати або на перший вільний елемент стеку, або на останній записаний в стек елемент. Однаково, який з цих двох варіантів вибрати, важливо надалі строго дотримуватися його при обробці стеку.

При занесенні елементу в стек елемент записується на місце, яке визначається покажчиком стеку, потім покажчик модифікується так, щоб він вказував на наступний вільний елемент (якщо покажчик вказує на останній записаний елемент,то спочатку модифікується покажчик, а потім проводиться запис елемента).Модифікація покажчика полягає в надбавці до нього або у відніманні від нього одиниці (стек росте у бік збільшення адреси).

Операція виключення елемента полягає в модифікації покажчика стеку (в напрямку,зворотному модифікації при включенні) і вибірці значення, на яке вказує покажчик стеку. Після вибірки комірка, в якій розміщувався вибраний елемент,вважається вільною.

Операція очищення стеку зводиться до запису в покажчик стеку початкового значення -адреси початку виділеної ділянки пам’яті.

Визначення розміру стека зводиться до обчислення різниці покажчиків: покажчика стеку й адреси початку ділянки.

При зв’язному представленні стеку кожен елемент стеку складається із значення і покажчика, який вказує на попередньо занесений у стек елемент. Зв’язне представлення викликає втрату пам’яті, що викликане наявністю покажчика в кожному елементі стеку, і представляє інтерес тільки у випадку, коли важко визначити максимальний розмір стеку.

Отже,для зв’язного представлення стеку потрібно, щоб кожен його елемент описувався структурою, яка поєднує дані і покажчик на наступний елемент.

Для виконання операцій над стеком потрібен один покажчик на вершину стеку.Створення пустого стеку полягатиме у присвоєнні покажчику на вершину нульового значення, що означатиме, що стек пустий.

Послідовність кроків для додавання елементу в стек складається з декількох кроків:

Виділити пам’ять під новий елемент стеку;
Занесення значення в інформаційне поле;
Встановлення зв’язку між ним і„старою” вершиною стеку;
Переміщення вершини стеку на новий елемент.

Вилученняелементу зі стеку також проводять за кілька кроків:

Зчитування інформації з інформаційного поля вершини стеку;
Встановлення на вершину стеку допоміжного покажчика;
Переміщення покажчика вершини стеку на наступний елемент;
Звільнення пам’яті, яку займає „стара” вершина стеку.

Черга

Чергою називається множина змінної кількості даних, над якою можна виконувати наступні операції:

Поповнення черги новими даними;
Перевірка, яка визначає чи пуста черга;
Перегляд перших добавлених даних;
Знищення самих перших доданих даних.

На основі такого функціонального опису, можна сформувати логічний опис. ЧергоюFIFO (First - In - First - Out - „першим прийшов - першим вийшов”). Називається такий послідовний список із змінній довжиною, в якому включення елементів виконується тільки з одного боку списку (хвіст черги), а виключення - з другого боку (голова черги).

Схематичне зображення черги

Основні операції над чергою - ті ж, що і над стеком - включення, виключення, визначення розміру, очищення, „неруйнуюче” читання.

При представленні черги вектором в статичній пам’яті на додаток до звичайних для опису вектора параметрів в ньому повинні знаходитися два покажчики: на голову і на хвіст черги. При включенні елемента в чергу елемент записується за адресою,яка визначається покажчиком на хвіст, після чого цей покажчик збільшується на одиницю. При виключенні елемента з черги вибирається елемент, що адресується покажчиком на голову, після чого цей покажчик зменшується на одиницю.

Очевидно,що з часом покажчик на хвіст при черговому включенні елемента досягне верхньої межі тієї ділянки пам’яті, яка виділена для черги. Проте, якщо операції включення чергувати з операціями виключення елементів, то в початковій частині відведеної під чергу пам’яті є вільне місце. Для того, щоб місця, займані виключеними елементами, могли бути повторно використані, черга замикається в кільце: покажчики (на початок і на кінець), досягнувши кінця виділеної області пам’яті, перемикаються на її початок. Така організація черги в пам’яті називається кільцевою чергою. Можливі, звичайно, і інші варіанти організації:наприклад, всякий раз, коли покажчик кінця досягне верхньої межі пам’яті, зсувати всі не порожні елементи черги до початку ділянки пам’яті, але як цей, так і інші варіанти вимагають переміщення в пам’яті елементів черги і менш ефективні,ніж кільцева черга.

У початковому стані покажчики на голову і хвіст вказують на початок ділянки пам’яті. Рівність цих двох покажчиків є ознакою порожньої черги. Якщо в процесі роботи з кільцевою чергою кількість операцій включення перевищує кількість операцій виключення, то може виникнути ситуація, в якій покажчик кінця„наздожене” покажчик початку. Це ситуація заповненої черги, але якщо в цій ситуації покажчики порівняються, ця ситуація буде така ж як при порожній черзі.Для розрізнення цих двох ситуацій до кільцевої черги пред’являється вимога, щоб між покажчиком кінця і покажчиком початку залишався „проміжок” з вільних елементів. Коли цей „проміжок” скорочується до одного елемента, черга вважається заповненою і подальші спроби запису в неї блокуються. Очищення черги зводиться до запису одного і того ж (не обов’язково початкового) значення в обидва покажчики. Визначення розміру полягає в обчисленні різниці покажчиків з урахуванням кільцевої природи черги.

При зв’язному представленні черги кожен елемент черги складається із значення іпокажчика, який вказує на попередньо занесений у чергу елемент.

Зв’язне представлення викликає втрату пам’яті, що викликане наявністю покажчика в кожному елементі черги, і представляє інтерес тільки у випадку, коли важко визначити максимальний розмір черги. Для зв’язного представлення черги потрібно, щоб кожен його елемент описувався структурою, яка поєднує дані і покажчик на наступний елемент.

Для виконання операцій над чергою потрібно два покажчики: на голову і хвіст черги.Створення пустої черги полягатиме у присвоєнні покажчикам на голову і хвістчерги нульових значень, що означатиме, що черга пуста.

Послідовність кроків для додавання елемента в кінець черги складається з декількох кроків:

Виділити пам’ять під новий елемент черги;
Занесення значення в інформаційне поле;
Занесення нульового значення в покажчик;
Встановлення зв’язку між ним і останнім елементом черги і новим, враховуючи випадок пустої черги;
Переміщення покажчика кінця черги на новий елемент.

Вилучення елементу з черги також проводять за кілька кроків:

Зчитування інформації з інформаційного поля голови черги;
Встановлення на голову черги допоміжного покажчика;
Переміщення покажчика початку черги на наступний елемент;
Звільнення пам’яті, яку займав перший елемент черги.

В реальних задачах іноді виникає необхідність у формуванні черг, відмінних від приведених структур. Порядок вибірки елементів з таких черг визначається пріоритетами елементів. Пріоритет в загальному випадку може бути представлений числовим значенням, яке обчислюється або на підставі значень яких-небудь полів елемента, або на підставі зовнішніх чинників. Так попередньо наведені структури стек і черги можна трактувати як пріоритетні черги, в яких пріоритет елемента залежить від часу його включення в структуру. При вибірці елемента всякий раз вибирається елемент з щонайбільшим пріоритетом.

Черги з пріоритетами можуть бути реалізовані на лінійних структурах - в суміжному або зв’язному представленні. Можливі черги з пріоритетним включенням- в яких послідовність елементів черги весь час підтримується впорядкованою,тобто кожний новий елемент включається на те місце в послідовності, яке визначається його пріоритетом, а при виключенні завжди вибирається елемент з голови. Можливі і черги з пріоритетним виключенням - новий елемент включається завжди в кінець черги, а при виключенні в черзі шукається (цей пошук може бути тільки лінійним) елемент з максимальним пріоритетом і після вибірки вилучається з послідовності. І в тому, і в іншому варіанті потрібний пошук, а якщо черга розміщується в статичній пам’яті - ще і переміщення елементів.

Деки

Дек - особливий вид черги. Дек (deq - double ended queue, тобто черга з двома кінцями) - це такий послідовний список, в якому як включення, так і виключення елементів, може здійснюватися з будь-якого з двох кінців списку. Так само можна сформулювати поняття деку, як стек, в якому включення і виключення елементів може здійснюватися з обох кінців.

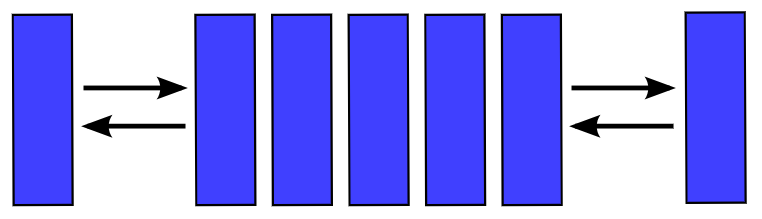
Схематичне зображення дека

Деки рідко зустрічаються у своєму первісному визначенні. Окремий випадок деку - дек з обмеженим входом і дек з обмеженим виходом. Логічна і фізична структури деку аналогічні логічній і фізичній структурі кільцевої черги. Проте, стосовно деку доцільно говорити не про голову і хвіст, а про лівий і правий кінець.

Над деком доступні наступні операції:

включення елемента праворуч;
включення елемента ліворуч;
виключення елемента з права;
виключення елемента з ліва;
визначення розміру;
очищення.

Фізична структура деку в статичній пам’яті ідентична структурі кільцевої черги.

Теми для самостійного вивчення

Реалізація множин на мові С++
Реалізація стеків на мові С++
Реалізація черг на мові С++

Контрольні питання

Що таке множина як структура даних? Які основні властивості множини?
Які основні операції визначені над множинами? Наведіть приклади.
Як можна реалізувати множину у мовах програмування C/C++?
Що таке таблиця як структура даних? Чим вона відрізняється від масиву?
Які особливості організації доступу до елементів таблиці за ключем?
Що таке стек? Які основні операції над стеком? Наведіть приклади використання.
Як реалізується стек у статичній та динамічній пам’яті?
Що таке черга? Які основні операції над чергою? У чому різниця між чергою та стеком?
Як організувати кільцеву чергу? Які її переваги?
Що таке дек? Які операції над деком можливі та в яких задачах він використовується?
Які переваги та недоліки зв’язного і масивного представлення стеків і черг?
Як визначити розмір і перевірити порожність для стеку, черги, деку?
Які типові помилки виникають при реалізації стеків, черг, деків?
Як організувати пріоритетну чергу? Де вона застосовується?
Які структури даних належать до абстрактних типів даних і чому?