Задача сортування. Стратегії сортування

Задача сортування

Для самого загального випадку задачу сортування формулюється: є деяка неврегульована вхідна множина ключів і потрібно отримати множину цих же ключів, впорядкованих за збільшенням або зменшенням.

Зі всіх задач програмування сортування, можливо, має найбагатший вибір алгоритмів розв’язку. Назвемо деякі чинники, які впливають на вибір алгоритму.

Наявний ресурс пам’яті: повинні вхідна й вихід множини розташовуватися в різних ділянках пам’яті, чи вихідна множина може бути сформована на місці вхідної. В останньому випадку наявна ділянка пам’яті повинна в ході сортування динамічно перерозподілятися між вхідною і вихідною множинами.
Початкова впорядкованість вхідної множини: у вхідній множині можуть попадатися впорядковані ділянки. В граничному випадку вхідна множина може виявитися вже впорядкованою. Одні алгоритми не враховують початкової впорядкованості і вимагають одного і того ж часу для сортування будь-якої множини даного обсягу, інші виконуються тим швидше, чим краще впорядкованість на вході.
Часові характеристики операцій: при визначенні порядку алгоритму час виконання вважається звичайно пропорційним кількості порівнянь ключів. Ясно, проте, що порівняння числових ключів виконується швидше, ніж стрічкових, операції пересилки, характерні для деяких алгоритмів, виконуються тим швидше, ніж менший об’єм записів. Залежно від характеристик запису таблиці може бути вибраний алгоритм, що забезпечує мінімізацію числа тих чи інших операцій.
Складність алгоритму. Простий алгоритм вимагає меншого часу для його реалізації і вірогідність помилки в реалізації його менше. При програмуванні вимоги дотримання термінів розробки і надійності продукту можуть навіть превалювати над вимогами ефективності функціонування.

Алгоритм сортування називається усталеним, якщо у відсортованому масиві він не змінює порядку розташування елементів.

Ефективність методів сортування визначається двома параметрами:

кількістю порівнянь;
кількістю пересилань елементів.

Різноманітність алгоритмів сортування вимагає деякої їхньої класифікації. Вибраний один з вживаних для класифікації підходів, орієнтований перш за все на логічні характеристики використовуваних алгоритмів. Згідно цьому підходу будь- який алгоритм сортування використовує одну з наступних чотирьох стратегій (або їхню комбінацію).

Стратегія вибірки. З вхідної множини вибирається наступний за критерієм впорядкованості елемент і включається в вихідну множину на наступне з місце.
Стратегія включення. З вхідної множини вибирається наступний за номером елемент і включається в вихідну множину на те місце, яке він повинен займати відповідно до критерію.
Стратегія розподілу. Вхідна множина розбивається на ряд підмножин і сортування ведеться у середині кожної такої підмножини.
Стратегія злиття. Вихідна множина отримується шляхом злиття маленьких впорядкованих підмножин.

Класифікації алгоритмів

Порівняльні алгоритми:
- Сортування бульбашкою (Bubble Sort): Сортує елементи, порівнюючи їх попарно і міняючи місцями, якщо вони не відсортовані.
- Сортування вибіркою (Selection Sort): Вибирає найменший (або найбільший) елемент і поміщає його на правильне місце.
- Сортування вставками (Insertion Sort): Порівнює кожен елемент із відсортованою частиною і вставляє його на правильне місце.
Не порівняльні алгоритми:
- Сортування підрахунком (Counting Sort): Ефективний для сортування цілих чисел, якщо діапазон значень обмежений.
- Сортування підрахунком (Radix Sort): Використовується для сортування цілих чисел, розглядаючи їх бітове представлення.
Рекурсивні алгоритми:
- Швидке сортування (Quicksort): Рекурсивно розбиває масив на менші частини і сортує їх.
- Сортування злиттям (Merge Sort): Рекурсивно розбиває масив пополовині, сортує кожну половину, а потім об’єднує їх.
Сортування на місці (In-Place Sorting):
- Сортування бульбашкою (Bubble Sort): Має низький об’єм пам’яті, оскільки сортування відбувається на місці, без додаткового масиву.
Адаптивні алгоритми:
- Сортування вставками (Insertion Sort): Ефективний для вже частково відсортованих масивів, оскільки вставка нового елемента не вимагає багато операцій.
Стійкі алгоритми сортування:
- Сортування бульбашкою (Bubble Sort): Міняє тільки сусідні елементи, тобто два однакові елементи не будуть обмінюватися.

Стратегії сортування

Сортування розподілом

Алгоритм порозрядного сортування вимагає представлення ключів сортованої послідовності у вигляді чисел в деякій системі числення P. Число проходів сортування рівно максимальному числу значущих цифр в числі - D. При кожному проході аналізується значуща цифра в черговому розряді ключа, починаючи з молодшого розряду. Всі ключі з однаковим значенням цієї цифри об’єднуються в одну групу. Ключі в групі розташовуються в порядку їхнього надходження. Після того, як вся початкова послідовність розподілена по групах, групи розташовуються в порядку зростання пов’язаних з групами цифр. Процес повторюється для другої цифри і т.д., поки не будуть вичерпані значущі цифри в ключі. Основа системи числення P може бути будь-якою при цьому потрібно P груп.

Порядок алгоритму якісно лінійний - O(N), для сортування потрібно _D*N_операцій аналізу цифри. Проте, в такій оцінці порядку не враховується ряд обставин.

По-перше, операція виділення значущої цифри буде простою і швидкою тільки при P=2, для інших систем числення ця операція може вимагати значно більше часу, ніж операція порівняння.

По-друге, при оцінці алгоритму не враховуються затрати часу і пам’яті на створення і ведення груп. Розміщення груп в статичній робочій пам’яті вимагає пам’яті для P*N елементів, оскільки в граничному випадку всі елементи можуть потрапити в якусь одну групу. Якщо ж формувати групи усередині тієї ж послідовності за принципом обмінних алгоритмів, то виникає необхідність перерозподілу послідовності між групами і всі проблеми і недоліки, властиві алгоритмам включення. Найбільш раціональним є формування груп у вигляді зв’язних списків з динамічним виділенням пам’яті.

Алгоритм швидкого сортування Хоара відноситься до розподільних і забезпечує показники ефективності O(N*log2(N)) навіть при якнайгіршому початковому розподілі.

Використовується два індекси з початковими значеннями початку і кінця множини відповідно. Ключ початку порівнюється з ключем кінця. Якщо ключі задовольняють критерію впорядкованості, то індекс кінця зменшується на 1 і проводиться наступне порівняння. Якщо ключі не задовольняють критерію, то записи міняються місцями. При цьому індекс кінця фіксується і починає мінятися індекс початку (збільшуватися на 1 після кожного порівняння). Після наступної перестановки фіксується початок і починає змінюватися кінець і т.д. Прохід закінчується, коли індекси стають рівними. Запис, що знаходиться на позиції зустрічі індексів, стоїть на своєму місці в послідовності. Цей запис ділить послідовність на дві підмножини. Всі записи, розташовані ліворуч від неї мають ключі, менші ніж ключ цього запису, всі записи праворуч - більші. Той же самий алгоритм застосовується до лівої підмножини, а потім до правої. Записи підмножини розподіляються на дві менші підмножини і так далі. Розподіл закінчується, коли отримана підмножина буде складатися з єдиного елемента - така підмножина вже є впорядкованою.

Сортування злиттям

Алгоритми сортування злиттям, як правило, мають порядок O(N*log2(N)), але відрізняються від інших алгоритмів більшою складністю і вимагають великої кількості пересилок. Алгоритми злиття застосовуються в основному, як складова частина зовнішнього сортування.

При сортуванні попарним злиттям вхідна множина розглядається, як послідовність підмножин, кожна з яких складається з єдиного елемента і, отже, є вже впорядкованим. На першому проході кожні дві сусідні одноелементних множини зливаються в одну двоелементну впорядковану множину. На другому проході двоелементні множини зливаються в 4-елементні впорядковані множини і т.д. Врешті-решт отримують одну велику впорядковану множину.

Самою найважливішою частиною алгоритму є злиття двох впорядкованих множин. Цю частину алгоритму опишемо більш детально.

Початкові установки. Визначити довжини першої і другої початкових множин - l1 і l2 відповідно. Встановити індекси поточних елементів в початковій множині і1 і і2 в 0. Встановити індекс в вихідній множині j=1.
Цикл злиття. Виконувати крок 3 до тих пір, поки і1<=11 і і2<=12.
Порівняння. Порівняти ключ і1-го елемента з першої початкової множини з ключем і2-го елемента з другої початкової множини. Якщо ключ елемента з 1 -ої множини менший, то записати і1-тий елемент з 1-ої множини на j-те місце в вихідній множині і збільшити і1 на 1. Інакше - записати і2-тий елемент з 2-ої множини на j-те місце в вихідній множині і збільшити і2 на 1. Збільшити j на 1.
Виведення залишків. Якщо і1<=11, то переписати частину 1-ої початкової множини від і1 до l1 включно в вихідну множину. Інакше - переписати частину 2-ої початкової множини від і2 до l2 включно в вихідну множину.

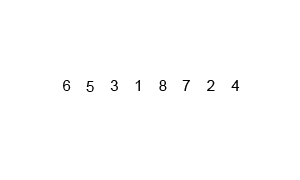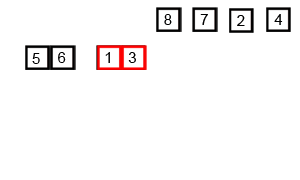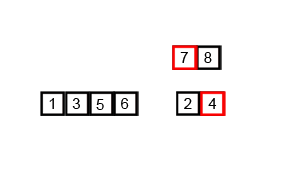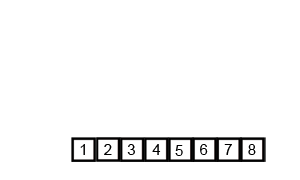
Сортування вибіркою

Даний метод реалізує практично “дослівно” стратегію вибірки. При програмній реалізації алгоритму виникає проблема значення ключа “порожньо”. Досить часто програмісти використовують в якості такого деяке явно відсутнє у вхідній послідовності значення ключа. Інший підхід - створення окремого вектора, кожний елемент якого має логічний тип і відображає стан відповідного елемента вхідної множини.

Алгоритм сортування простою вибіркою рідко застосовується. Набагато частіше застосовується його обмінний варіант. При обмінному сортуванні вибіркою вхідна і вихід множини розташовуються в одній і тій же ділянці пам’яті; вихідна - на початку ділянки, вхідна - в тій частині, що залишилася. У початковому стані вхідна множина займає всю ділянку, а вихідна множина - порожня. У міру виконання сортування вхідна множина звужується, а вихідна - розширяється.

Принцип методу полягає в наступному. Знаходять і вибирають в масиві елементів елемент з мінімальним значенням на інтервалі від першого до останнього елемента і міняють його місцями з першим елементом. На другому кроці знаходять елемент з мінімальним значенням на інтервалі від другого до останнього елемента і міняють місцями його з другим елементом. І так далі для всіх елементів.

Очевидно, що обмінний варіант забезпечує економію пам’яті та при його реалізації не виникає проблема “порожнього” значення. Загальна кількість порівнянь зменшується удвічі - N*(N-1)/2, але порядок алгоритму залишається степеневим. Кількість перестановок N-1, але перестановка удвічі більше потребує часу, ніж пересилка в попередньому алгоритмі.

Досить проста модифікація алгоритму обмінного сортування вибіркою передбачає пошук в одному циклі перегляду вхідної множини відразу і мінімуму, і максимуму, і обмін їх з першим і з останнім елементами множини відповідно. Хоча сумарна кількість порівнянь і пересилок в цій модифікації не зменшується, досягається економія на кількості ітерацій зовнішнього циклу.

Приведені вище алгоритми сортування вибіркою практично нечутливі до початкової впорядкованості. В будь-якому випадку пошук мінімуму вимагає повного перегляду вхідної множини. В обмінному варіанті початкова впорядкованість може дати деяку економію на перестановках для випадків, коли мінімальний елемент знайдений на першому місці у вхідній множині.

Ще один варіант такого сортування - сортування бульбашкою. При перегляді вхідної множини попарно порівнюються сусідні елементи множини. Якщо порядок їхнього проходження не відповідає заданому критерію впорядкованості, то елементи міняються місцями. В результаті одного такого перегляду при сортуванні за збільшенням елементів елемент з найбільшим значенням ключа переміститься (“спливе) на останнє місце в множині. При наступному проході на своє місце “спливе” другий за величиною ключа елемент і т.д. Вихідна множина, таким чином, формується в кінці сортованої послідовності, при кожному наступному проході його об’єм збільшується на 1, а об’єм вхідної множини зменшується на 1.

Порядок сортування бульбашкою - O(N2). Середнє число порівнянь - N*(N- 1)/2 і таке ж середня кількість перестановок, що значно гірше, ніж для обмінного сортування простим вибором. Проте, та обставина, що тут завжди порівнюються і переміщаються тільки сусідні елементи, робить сортування бульбашкою зручним для обробки зв’язних списків.

Ще одна перевага сортування бульбашкою полягає в тому, що при незначних модифікаціях її можна зробити чутливою до початкової впорядкованості вхідної множини.

Ще одна модифікація сортування бульбашкою носить назву шейкер- сортування. Суть її полягає в тому, що напрями переглядів чергують: за проходом до кінця множини слідує прохід від кінця до початку вхідної множини. При перегляді в прямому напрямку запис з найбільшим ключем ставиться на своє місце в послідовності, при перегляді у зворотному напрямі - запис з самим меншим. Цей алгоритм досить ефективний для задач відновлення впорядкованості, коли початкова послідовність вже була впорядкована, але піддалася не дуже значним змінам. Впорядкованість в послідовності з одиночною зміною буде гарантовано відновлена усього за два проходи.

Сортування Шелла - ще одна модифікація сортування бульбашкою. Суть її полягає в тому, що тут виконується порівняння ключів, віддалених один від одного на деяку відстань d. Початковий розмір d звичайно вибирається рівним половині загального розміру сортованої послідовності. Виконується сортування бульбашкою з інтервалом порівняння d. Потім величина d зменшується удвічі і знов виконується сортування бульбашкою, далі d зменшується ще удвічі і т.д. Останнє сортування бульбашкою виконується при d=1. Якісний порядок сортування Шелла залишається (N2), середнє ж число порівнянь, визначене емпіричним шляхом, - N*log2(N)^2. Прискорення досягається за рахунок того, що виявленні “не на місці” елементи при d>1, швидше “спливають” на свої місця.

Сортування включенням

Цей метод - “дослівна” реалізації стратегії включення. Порядок алгоритму сортування простим включенням - O(N2), якщо враховувати тільки операції порівняння. Але сортування вимагає ще й в середньому N2/4 переміщень, що робить її в такому варіанті значне менш ефективною, ніж сортування вибіркою.

Ефективність алгоритму може бути дещо поліпшена при застосуванні не лінійного, а дихотомічного пошуку. Проте, слід мати на увазі, що таке збільшення ефективності може бути досягнуте лише на значній кількості елементів. Так як алгоритм вимагає великої кількості пересилок, при значному обсязі одного запису ефективність може визначатися не кількістю операцій порівняння, а кількістю пересилок.

Реалізація алгоритму обмінного сортування простими вставками відрізняється від базового алгоритму тільки тим, що вхідна і вихідна множина розміщені в одній ділянці пам’яті.

Бульбашкове сортування включенням - це модифікація обмінного варіанту сортування. В цьому методі вхідна і вихід множини знаходяться в одній послідовності, причому вихід - в початковій її частині. В початковому стані можна вважати, що перший елемент послідовності вже належить впорядкованій вихідній множині, інша частина послідовності - невпорядкована. Перший елемент вхідної множини примикає до кінця вихідної множини. На кожному кроці сортування відбувається перерозподіл послідовності: вихідна множина збільшується на один елемент, а вхідна - зменшується. Це відбувається за рахунок того, що перший елемент вхідної множини тепер вважається останнім елементом вихідної. Потім виконується перегляд вихідної множини від кінця до початку з перестановкою сусідніх елементів, які не відповідають критерію впорядкованості. Перегляд припиняється, коли припиняються перестановки. Це приводить до того, що останній елемент вихідної множини “випливає” на своє місце в множині. Оскільки при цьому перестановка приводить до зсуву нового в вихідній множині елемента на одну позицію ліворуч, немає сенсу кожен раз проводити повний обмін між сусідніми елементами - достатньо зсовувати старий елемент праворуч, а новий елемент записати в вихідну множину, коли його місце буде встановлено.

Хоча обмінні алгоритми стратегії включення і дозволяють скоротити число порівнянь за наявності деякої початкової впорядкованості вхідної множини, значна кількість пересилок істотно знижує ефективність цих алгоритмів. Тому алгоритми включення доцільно застосовувати до зв’язних структур даних, коли операція перестановки елементів структури вимагає не пересилки даних в пам’яті, а виконується способом корекції покажчиків.

Турнірний метод сортування отримав свою назву через схожість з кубковою системою проведення спортивних змагань: учасники змагань розбиваються на пари, в яких розігрується перший тур; з переможців першого туру складаються пари для розіграшу другого туру і т.д. Алгоритм сортування складається з двох етапів. На першому етапі будується дерево: аналогічне схемі розіграшу кубка.

Алгоритм сортування впорядкованим бінарним деревом складається з побудови впорядкованого бінарного дерева і подальшого його обходу. Якщо немає необхідності в побудові всього лінійного впорядкованого списку значень, то немає необхідності і в обході дерева, в цьому випадку застосовується пошук у впорядкованому бінарному дереві. Відзначимо, що порядок алгоритму - O(N*log2(N)), але в конкретних випадках все залежить від впорядкованості початкової послідовності, який впливає на ступінь збалансованості дерева і нарешті - на ефективність пошуку.

Заслуговує на увагу модифікація цього алгоритму запропонована Р.Флойдом. Метод сортування за допомогою прямої вибірки базується на повторних пошуках найменшого ключа серед N елементів, серед тих що залишилися N-1 елементів і так далі. Удосконалити такий метод сортування можна залишаючи після кожного проходу більше інформації, ніж просто ідентифікація єдиного мінімального елемента. Наприклад, виконавши n/2 порівнянь, можна визначити в кожній парі ключів менший. За допомогою n/4 порівнянь - менший із пари вже вибраних менших і так далі. Провівши n-1 порівнянь, можна побудувати дерево вибору і ідентифікувати його корінь як потрібний найменший ключ.

Другий етап сортування - спуск вздовж шляху, відміченого найменшим елементом, і виключення його з дерева шляхом заміни або на пустий елемент (дірку) в самому низу, або на елемент із сусідньої гілки в проміжних вершинах. Елемент, який перемістився в корінь дерева, знову буде найменшим (тепер вже другим) ключем, і його можна виключити. Після n таких кроків дерево стане пустим і процес сортування завершується.

Звичайно, хотілося б позбавитися дірок, якими в кінцевому рахунку буде заповнене все дерево і які породжують багато непотрібних порівнянь. Крім того, потрібно знайти б таке представлення дерева з n елементів, яке потребує лише n одиниць пам’яті.

Р. Флойдом був запропонований деякий “лаконічний” спосіб побудови піраміди “на тому ж місці”, який використовує функцію зсуву елементів початкового вектора.

Сортування частково впорядкованим бінарним деревом також належить до цієї групи сортування. У бінарному дереві, яке будується при цьому для кожного вузла справедливе наступне твердження: значення ключа, записане у вузлі, менше, ніж ключі його нащадків. Для повністю впорядкованого дерева є вимоги до співвідношення між ключами нащадків. Для даного дерева таких вимог немає, тому таке дерево і називається частково впорядкованим. Крім того, таке дерево повинно бути абсолютно збалансованим. Це означає не тільки те, що довжини шляхів до будь-якого двох листків розрізняються не більш, ніж на 1, але і те, що при додаванні нового елемента в дерево перевага завжди віддається лівій гілці, поки це не порушує збалансованість.

Для сортування цим методом потрібно визначити дві операції: вставка в дерево нового елемента і вибірка з дерева мінімального елемента; причому виконання будь-якій з цих операцій не повинне порушувати ні сформульованої вище часткової впорядкованості дерева, ні його збалансованості.

Якщо застосовувати сортування частково впорядкованим деревом для впорядкування вже готової послідовності розміром N, то необхідно N раз виконати вставку, а потім N раз - вибірку. Порядок алгоритму - O(N*log2(N)), але середнє значення кількості порівнянь приблизно в 3 рази більше, ніж для турнірного сортування. Але сортування частково впорядкованим деревом має одну істотну перевагу перед всіма іншими алгоритмами - це найзручніший алгоритм для “сортування on-line”, коли сортована послідовність не зафіксована до початку сортування, а міняється в процесі роботи і вставки чергують з вибірками. Кожна зміна (додавання елемента) сортованої послідовності вимагає тут не більш, ніж 2*log2(N) порівнянь і перестановок, в той час, як інші алгоритми вимагають при одиничній зміні нового впорядковування всієї послідовності “за повною програмою”.

Теми для самостійного вивчення

Принципи роботи алгоритмів групи CRC
Принципи роботи алгоритмів групи MD
Принципи роботи алгоритмів групи SHA
Недоліки алгоритмів групи MD

Контрольні питання

Що таке хеш-функція?
Яке призначення хеш-функцій?
Які алгоритми хешування ви знаєте?
В чому головна відмінність процесів хешування та шифрування?